] Let {an} be a convergent sequence of real numbers and let lim a, = a. n00 (a) Prove that {a,} is bounded. (b) Use the definition of the limit of a sequence to show that lim (an)² = a². %3D
] Let {an} be a convergent sequence of real numbers and let lim a, = a. n00 (a) Prove that {a,} is bounded. (b) Use the definition of the limit of a sequence to show that lim (an)² = a². %3D
Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter10: Sequences, Series, And Probability
Section: Chapter Questions
Problem 8RE
Related questions
Topic Video
Question
![] Let {an} be a convergent sequence of real numbers and let lim a, = a.
n00
(a) Prove that {a,} is bounded.
(b) Use the definition of the limit of a sequence to show that lim (an)² = a².
%3D](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F6c58f7ac-1edf-4750-a4d7-5aacd23f668a%2F6e9e320d-5d9b-4b25-acd6-bf6fed592ddd%2Fwj4eyamk.jpeg&w=3840&q=75)
Transcribed Image Text:] Let {an} be a convergent sequence of real numbers and let lim a, = a.
n00
(a) Prove that {a,} is bounded.
(b) Use the definition of the limit of a sequence to show that lim (an)² = a².
%3D
Expert Solution
Step 1

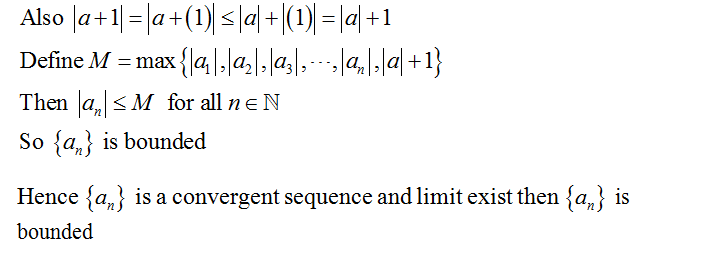
Step by step
Solved in 2 steps with 4 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage


College Algebra
Algebra
ISBN:
9781305115545
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage


College Algebra
Algebra
ISBN:
9781305115545
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning