Introduction To Finite Element Analysis And Design
2nd Edition
ISBN: 9781119078722
Author: Kim, Nam H., Sankar, Bhavani V., KUMAR, Ashok V., Author.
Publisher: John Wiley & Sons,
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 2, Problem 26E
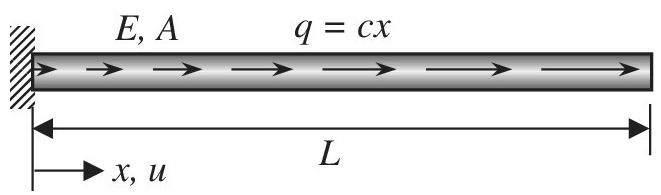
Consider the uniform bar in the figure. Axial load q is linearly distributed along the length of the bar according to
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Figure below shows the bar with three equal elements. Use the finite element method and calculate:
2.1 the global stiffness matrix
2.2 the displacement on node 2, 3, 4
2.3 the Strain in each element
2.4 the stresses in each element using Hook's law and compare with theoretical stresses (o=F/A)
(1)
(2)
(3)
-50 N
10 mm
10 mm
10 mm
A1=50 mm?
A2=20 mm?
A:=10 mm?
E=200 GPa
A very thick structure is subjected to certain traction boundary conditions
on its surface. The cross-section and the applied load do not vary with the z-coordinate. The
following stress function is proposed for this problem:
-y
p(x,y) = Sin (x) (A x²e + B e")
(i) use the biharmonic equation to find restrictions, if any, on values of A and B
(ii) calculate all stress components
(iii) calculate all strain components in terms of A, B, and C as well as the Young modulus and
Poisson's ratio E and y, respectively.
(iv) check that the equilibrium equations are satisfied
(v) determine the traction boundary conditions at x =± a and
y=+b
A bar of a uniform cross-section is rigidly fixed at one end and loaded by an off-centre tensile point load F = 2.5 kN at the other end, see Fig. Q1a. The Figure Q1b presents the view of the beam from the free end where the point of application of the load F is indicated as A. The allowable stress [σ]=269 MPa
The geometrical parameters are given as follow
h=17 mm , b=48 mm
the magnitude of the maximum normal stress in the beam and where within the beam it is achieved.
a) Find the bending moment relative to z-axis Mz on the cross section
b) Find the bending moment relative to y-axis My on the cross section
c)The second moment of area relatve to z-axis
d)The second moment of area relative to y-axis
e) The magnitude of the maximum normal stress in the beam
f)The magnitude of the minimum normal stress in the beam
Chapter 2 Solutions
Introduction To Finite Element Analysis And Design
Ch. 2 - Answer the following descriptive questions.
a....Ch. 2 - Use the Galerkin method to solve the following...Ch. 2 - Solve the differential equation in problem 2 using...Ch. 2 - Prob. 4ECh. 2 - Using the Galerkin method, solve the following...Ch. 2 - A one-dimensional heat conduction problem can be...Ch. 2 - Solve the one-dimensional heat conduction problem...Ch. 2 - Prob. 8ECh. 2 - Solve the differential equation in problem 8 for...Ch. 2 - Prob. 10E
Ch. 2 - Prob. 11ECh. 2 - Prob. 12ECh. 2 - Using the Galerkin method, calculate the...Ch. 2 - The boundary-value problem for a clamped-clamped...Ch. 2 - The boundary-value problem for a cantilevered beam...Ch. 2 - Prob. 16ECh. 2 - Consider a finite element with three nodes, as...Ch. 2 - A vertical rod of elastic material is fixed at...Ch. 2 - A bar in the figure is under the uniformly...Ch. 2 - Prob. 20ECh. 2 - A tapered bar with circular cross section is fixed...Ch. 2 - The stepped bar shown in the figure is subjected...Ch. 2 - A bar shown in the figure is modeled using three...Ch. 2 - Consider the tapered bar in problem 17. Use the...Ch. 2 - Consider the tapered bar in problem 21. Use the...Ch. 2 - Consider the uniform bar in the figure. Axial load...Ch. 2 - Determine shape functions of a bar element shown...Ch. 2 - Consider a finite element with three nodes, as...
Additional Engineering Textbook Solutions
Find more solutions based on key concepts
A particle travels along a straight line with an acceleration of a = (10 0.2s) m/s2, where s is measured in me...
Engineering Mechanics: Dynamics (14th Edition)
When a valve is closed suddenly in a pipe with flowing water, a water hammer pressure wave is set up. The very ...
Fox and McDonald's Introduction to Fluid Mechanics
The data shown in the following graph was collected during testing of an electromagnetic mass driver. The energ...
Thinking Like an Engineer: An Active Learning Approach (3rd Edition)
A barge is 60 ft long, 20 ft wide, and 8 ft deep. When empty, it weighs 210000 lb, and its center of gravity is...
Applied Fluid Mechanics (7th Edition)
A bicyclist applies a 40-N force to the brake lever of her bicycle as shown. Determine the corresponding tensio...
Engineering Mechanics: Statics
The expression for the rate at which useful heat is collected per unit area of the collector and also find the ...
Introduction to Heat Transfer
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- A wine of length L = 4 ft and diameter d = 0.125 in. is stretched by tensile forces P = 600 lb. The wire is made of a copper alloy having a stress-strain relationship that may be described mathematically by =18,0001+30000.03(=ksi) in which is nondimensional and has units of kips per square inch (ksi). (a) Construct a stress-strain diagram for the material. (bj Determine the elongation, of the wire due to the Forces P. (c) IF the forces are removed, what is the permanent set of the bar? (d) If the forces are applied again, what is the proportional limit?arrow_forwardSolve the preceding problem if the cross- sectional dimensions are b = 1.5 in. and h = 5.0 in., the gage angle is ß = 750, the measured strains are = 209 × 10-6 and B = -110 × 10, and the material is a magnesium alloy with modulus E = 6.0 X 106 psi and Poisson’s ratio v = 0.35.arrow_forwardA round bar ABC of length 2L (see figure) rotates about an axis through the midpoint C with constant angular speed w (radians per second). The material of the bar has weight density y. (a) Derive a formula for the tensile stress a’ in the bar as a function of the distance x from the midpoint C. (b) What is the maximum tensile stress a max?arrow_forward
- Solve the preceding problem for the following data:P = 160 kN,JV = 200 tN,L = 2 m,b = 95 mm, h = 300 mm, and d = 200 mmarrow_forwardSolve the preceding problem for the following data: b = 8.0 in., k = 16 lb/in., a = 45°, and P = 10 lb.arrow_forwardAn aluminum bar subjected to tensile Forces P has a length L = 150 in. and cross-sectional area A = 2.0 in2 The stress-strain behavior of the aluminum may be represented approximately by the bilinear stress-strain diagram shown in the figure. Calculate the elongation S of the bar for each of the following axial loads: p = 8 kips, 16 kips. 24 kips, 32 kips, and 40 kips. From these results, plot a diagram of load P versus elongation S (load-displacement diagram).arrow_forward
- An clement of material in plane strain (see figure) is subjected to strains ex= 480 × 10-6, Ey= 70 × l0-6, and yxy= 420 × l0-6. Determine the following quantities: (a) the strains for an element oriented at an angle 0 = 75°, (b) the principal strains, and (c) the maximum shear strains. Show the results on sketches of properly oriented elements.arrow_forwardA prismatic bar in tension has a length L = 2.0 m and cross-sectional area A =249 mn2. The material of the bar has the stress-strain curve shown in the figure. Determi ne t he elongation 5 of the bar for each of the following axial loads: P = 10 kN, 20 kN, 30 kN, 40 kN. and 45 kN. From these results, plot a diagram of load P versus elongation 5 (load-displacement diagram).arrow_forwardA circular aluminum tube of length L = 600 mm is loaded in compression by forces P (see figure). The outside and inside diameters are d2= 75 mm and d1= 63 mm, respectively. A strain gage is placed on the outside of the lube to measure normal strains in the longitudinal direction. Assume that E = 73 GPa and Poissons ratio is v = 0.33. (a) IF the compressive stress in the tube is 57 MPa, what is the load P? (b) If the measured strain is e = 78 J X 10-6, what is the shorteningarrow_forward
- -11 A solid steel bar (G = 11.8 X 106 psi ) of diameter d = 2,0 in. is subjected to torques T = 8.0 kip-in. acting in the directions shown in the figure. Determine the maximum shear, tensile, and compressive stresses in the bar and show these stresses on sketches of properly oriented stress elements. Determine the corresponding maximum strains (shear, tensile, and compressive) in the bar and show these strains on sketches of the deformed elements.arrow_forwardA bar with a circular cross section having two different diameters d and 2d is shown in the figure. The length of each segment of the bar is L/2T and the modulus of elasticity of the material is E. (a) Obtain a formula for the strain energy U of the bar due to the load P. (b) Calculate the strain energy if the load P = 27 kN, the length L = 600 mm, the diameter d = 40 mm, and the material is brass with E = 105 GPa.arrow_forwardA uniformly tapered lube AB of circular cross section and length L is shown in the figure. The average diameters at the ends are dAand d£= 2d t. Assume E is constant. Find the elongation S of the tube when it is subjected to loads P acting at the ends. Use the following numerical data:^ = 35 mm, L = WO mm, E = 2.1 GPa. and P = 25 tN. Consider the following cases. (a) A hole of constant diameter dAis drilled from B toward A to form a hollow section of length x - U2. (b) A hole of variable diameter a\.x) is drilled, from B toward A to form a hollow section of length x = L/2 and constant thickness t = dA/20.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Lec21, Part 5, Strain transformation; Author: Mechanics of Materials (Libre);https://www.youtube.com/watch?v=sgJvz5j_ubM;License: Standard Youtube License