
Concept explainers
(a)
The plot of the logarithm of the rate of recrystallization versus the inverse of the absolute temperature and to check whether it is linear or not.
Answer to Problem 4.19P
The graph of logarithm of the rate of recrystallization versus the inverse of absolute temperature is shown in figure (1) and it is linear.
Explanation of Solution
Given:
The given table is,
| S. No. | Temperature |
Time (Seconds) |
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
392 | |
| |
|
|
Calculation:
Draw the table to plot the graph of logarithm of the rate of recrystallization versus the inverse of absolute temperature.
| S. No. | Temperature |
|
Time
|
Rate
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
392 | |
|
|
|
| |
|
|
|
|
|
The graph of logarithm of the rate of recrystallization versus the inverse of absolute temperature is shown below.
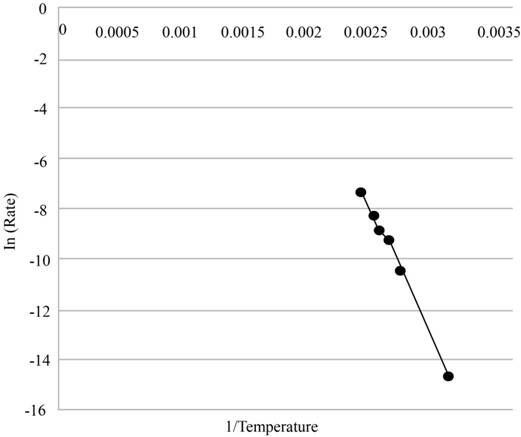
Figure (1)
Conclusion:
Therefore, the graph of logarithm of the rate of recrystallization versus the inverse of absolute temperature is shown in figure (1) and it is linear.
(b)
The activation enthalpy for the recrystallization of copper.
Answer to Problem 4.19P
The activation enthalpy for the recrystallization of copper is
Explanation of Solution
Formula Used,
The activation enthalpy for the recrystallization of copper is given by,
Here,
Calculation:
The activation enthalpy for the recrystallization of copper is calculated as,
Substitute
Conclusion:
Therefore, the activation enthalpy for the recrystallization of copper is
(c)
The reason for activation enthalpy of recrystallization of copper being less than the activation enthalpy for vacancy diffusion.
Answer to Problem 4.19P
The activation enthalpy for the recrystallization is less than the activation enthalpy for vacancy diffusion because during the process of recrystallization, the size of grains increases and the vacancy site decreases.
Explanation of Solution
Introduction:
The Gibbs free energy is the energy that is available or free, to do work under conditions of constant pressure and temperature.
The expression for the Gibb’s free energy is given by,
Here,
The term
Here,
During the process of recrystallization, the size of the grain changes to form a new crystal structure. By this process the grain size changes its size by diffusing into other grains, thereby increasing the size of the grains. When the size of the grain increases, the possibility for the vacancy site decreases; that’s why the activation enthalpy of recrystallization of copper is less than the activation enthalpy for vacancy diffusion.
Conclusion:
Therefore, the activation enthalpy for the recrystallization is less than the activation enthalpy for vacancy diffusion because during the process of recrystallization, the size of grains increases and the vacancy site decreases.
(d)
The temperature at which the copper completely crystallizes in
Answer to Problem 4.19P
The temperature at which the copper completely crystallizes in
Explanation of Solution
Formula Used,
The logarithmic rate of crystallization is given by,
Here,
Calculation:
The logarithmic rate of crystallization is calculated as,
Substitute
Drop a perpendicular from
Conclusion:
Therefore, the temperature at which the copper completely crystallizes in
Want to see more full solutions like this?
Chapter 4 Solutions
Materials Science And Engineering Properties
- In an engineering application, the material is a strip of iron with a fixed crystallographic structure subject to a tensile load during operation. The part failed (yielded) during operation and needs to be replaced with a component with better properties. You are told that two other iron strips had failed at yield stresses of 110 and 120 MPa, with grain sizes of 30 microns and 25 microns respectively. The current strip has a grain size of 20 microns. The diameter of the rod is 1 mm and the load applied is 100 N. What is the yield stress of the new part C and would you recommend it for operation? Select one: Oa. 133.5 MPa, yes O b. OC. Od Oe. 120.5 MPa, no 129.5, yes 140.5, no 123.5 MPa, yesarrow_forwardThe assembly consists of a brass shell (1) fully bonded to a ceramic core (2). The brass shell [E = 86 GPa, α= 18 × 10−6/°C] has an outside diameter of 33 mm and an inside diameter of 27 mm. The ceramic core [E = 320 GPa, α= 2.5 × 10−6/°C] has a diameter of 27 mm. At a temperature of 15°C, the assembly is unstressed. Assume L = 320 mm. Determine the largest temperature increase Δt that is acceptable for the assembly if the normal stress in the longitudinal direction of the brass shell must not exceed 65 MPa.arrow_forwardScission can be defined as. a. The loss of fragments from the surfaces of ceramic materials due to internal or residual stress b. An increase in the volume of a polymeric materials caused by the absorption of glass or liquid. c. The formation of crystalline regions in amorphous network ceramics. d. The fracture of long chain molecules in polymers subjected to neutron irradiation or radiation by ultraviolet lightarrow_forward
- Does the size of an ion affect the magnitude of the activity for varying ionic strengths? Does the activity coefficient depend on whether the ion is a cation or an anion?arrow_forwardWhich type of hardness can be removed by Boiling? Select one: a. Permanent and Temporanry Hardness b. Temporary Hardness C. None of the answers d. Permanent Hardnessarrow_forward2. In a copper-nickel system as shown in figure, an alloy composition of 35 wt% Ni was cooled down from the temperature of 1300°C. Sketch the expected microstructures at the point a, b, c, d and e and briefly describe the development of these microstructures in the equilibrium cooling. L. L (35 Ni) 1300 L (32 Ni) a (46 Ni) a(43 Ni) L (24 Ni) d 1200 1100 20 30 40 50 Composition (wt% Ni) Temperature (°C))arrow_forward
 Materials Science And Engineering PropertiesCivil EngineeringISBN:9781111988609Author:Charles GilmorePublisher:Cengage Learning
Materials Science And Engineering PropertiesCivil EngineeringISBN:9781111988609Author:Charles GilmorePublisher:Cengage Learning
