
Concept explainers
The speed of light in a medium of index of refraction
Show that the actual path is not necessarily one of minimum time. Hint: In the diagram,
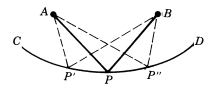
(a) Are the same length as the actual path if C D is an ellipse with
(b) Are longer than the actual path if C D is a line tangent at
(c) Are shorter than the actual path if C D is an are of a curve tangent to the ellipse at
(d) Are longer on one side and shorter on the other if C D crosses the ellipse at
Want to see the full answer?
Check out a sample textbook solution
Chapter 9 Solutions
Mathematical Methods in the Physical Sciences
Additional Math Textbook Solutions
A Survey of Mathematics with Applications (10th Edition) - Standalone book
Mathematics with Applications In the Management, Natural and Social Sciences (11th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
The Heart of Mathematics: An Invitation to Effective Thinking
Introductory Mathematics for Engineering Applications
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
